# 树的深度优先遍历与广度优先遍历

# 1. 递归遍历

• 前序遍历：根结点 ---> 左子树 ---> 右子树
• 中序遍历：左子树---> 根结点 ---> 右子树
• 后序遍历：左子树 ---> 右子树 ---> 根结点

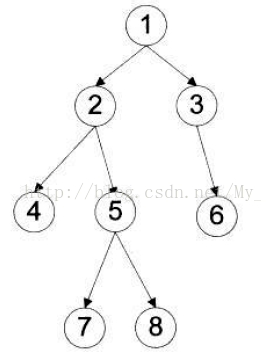
• 前序遍历：1 2 4 5 7 8 3 6
• 中序遍历：4 2 7 5 8 1 3 6
• 后序遍历：4 7 8 5 2 6 3 1

    // 前序遍历：根结点 ---> 左子树 ---> 右子树（常用的深度优先遍历）
    function recursion(root) {
        if (!root) return
    
        let { left, right, val } = root
        console.log(val, '递归：前序遍历，先访问根节点')
        recursion(left)
        recursion(right)
    }
    
    // 中序遍历：左子树---> 根结点 ---> 右子树
    function recursion(root) {
        if (!root) return
    
        let { left, right, val } = root
        recursion(left)
        console.log(val, '递归：中序遍历')
        recursion(right)
    }
    
    // 后序遍历：左子树 ---> 右子树 ---> 根结点
    function recursion(root) {
        if (!root) return
    
        let { left, right, val } = root
        recursion(left)
        recursion(right)
        console.log(val, '递归：后序遍历')
    }
    

变通：给定一个二叉树，返回所有从根节点到叶子节点的路径？ 答案 (opens new window) (opens new window)

# 2. 基于栈的深度优先

栈：后进先出，适合先深度left,中间的right都保存到栈中

以下代码都是基于栈数据结构的前序遍历（前序遍历最好理解）

    // 假设节点：Node { left, right, val}
    function DFS_By_Stack(root) {
        // 方法一：栈，后进先出，
        if (root === null) return []
    
        let stack = [root]
        while(stack.length) {
            let { left, right, val } = stack.pop()
            console.log(val, 'serach by dfs')
            right && stack.push(right) // 先把right存入栈中
            left && stack.push(left)
        }
    
        // 方法二：变种的栈实现DFS（js语言中，数组同时实现了队列和栈）
        if(root == null) return []
    
        let stack = [root]
        while(stack.length) {
            let { left, right, val } = stack.shift()
            console.log(val, 'serach by dfs')
            right && queue.unshift(right)
            left && queue.unshift(left)
        }
    
        // 方法三：通用栈，本质上和方法一是一样的
        if (root === null) return
    
        let stack = []
        let currentNode = root
        while(currentNode) {
            let { left, right, val } = currentNode
            console.log(val, 'serach by dfs')
            right && stack.push(right) // 先把right存入栈中
            if (left) {
                currentNode = left // 关键，left一条道走到黑
            } else {
                currentNode = stack.pop()
            }
        }
    }
    

# 3. 基于队列的广度优先

    function BFS_By_Queue(root) {
        if (root === null) return
    
        let queue = [root]
        while(queue.length) {
            let { left, right, val } = queue.shift() // 队列，先进先出。先遍历顶层节点
            console.log(val, 'serach by bfs')
            left && queue.push(left)
            right && queue.push(right)
        }
    }
    

变通：计算二叉树的最大深度？ 答案 (opens new window) (opens new window)

# 4. 思考题

思考题： Node节点变为{ val, children} （更符合现实案例）

// 基于变种队列的深度优先搜索：（得益于js语言 array数组同时集成了队列和栈）

    // 使用变种的queue实现，非常简单
    function DFS_Search_By_Variety_Queue(searchVal) {
        let queue = [root]
    
        while(queue.length) {
            let { val, children } = queue.shift()
    
            if(val === searchVal) return true
            else queue.unshift(...children) // children插入到队列前头
        }
    
        return false
    }
    

基于队列的广度优先搜索：

    // 使用纯正queue实现，也非常简单
    function BFS_Search_By_Pure_Queue(searchVal) {
        let queue = [root]
    
        while(queue.length) {
            let { val, children } = queue.shift()
    
            if(val === searchVal) return true
            else queue.push(...children) // children插入到队列后头
        }
    
        return false
    }
    

# 参考资料

• https://medium.com/@kenny.hom27/breadth-first-vs-depth-first-tree-traversal-in-javascript-48df2ebfc6d1
• https://blog.csdn.net/My_Jobs/article/details/43451187