# 排序算法

# 1. 冒泡排序

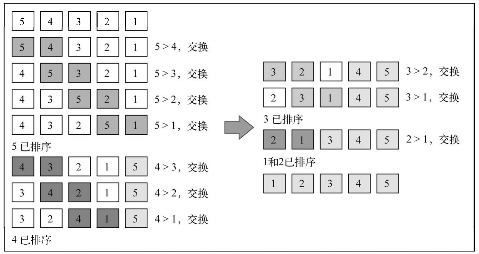
所有排序算法中最简单的，但不实用。因为时间复杂度：O(n2)。

数组中有 n 个数，比较每相邻两个数，如果前者大于后者，就把两个数交换位置；这样一来，第一轮就可以选出一个最大的数放在最后面；那么经过 n-1（数组的 length - 1） 轮，就完成了所有数的排序。

    // 从小到大冒泡排序
    function bubbleSort(arr) {
        for (var i = 0; i < arr.length - 1 ; i++) { // 两两比较，所以是arr.length - 1
            for(var j = 0; j < arr.length - i - 1 ; j++) {
                if (arr[j] > arr[j+1]) {
                    swap(arr, j, j+1)
                }
            }
        }
        return arr
    }
    
    function swap(arr, index1, index2) {
        var temp = arr[index1]
        arr[index1] = arr[index2]
        arr[index2] = temp
    }
    
    // 优化
    function bubbleSort(arr) {
        var max = arr.length - 1;
        for(var i = 0; i < max; i++) {
            var done = true // 声明一个变量，作为标志位
            for (var j = 0; j < max - i; j++) {
                if (arr[j] > arr[j + 1]) {
                    swap(arr, j, j+1)
                    done = false
                }
            }
            // 如果标记在某一排序中没有变动，即都正序了，可跳出循环
            if (done) {
                break
            }
        }
        return arr
    }
    

# 2. 选择排序

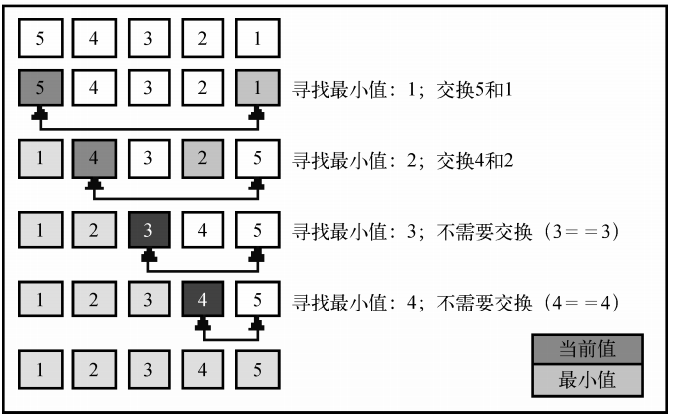
一种原址比较排序，每次找到最小值，并放在第一位，接着找接下里的最小值，放在第二位。时间复杂度：O(n2)。

    function selectionSort(arr) {
        var minIndex = 0
        for (var i = 0; i < arr.length - 1; i++) { // i作为currentIndex
            minIndex = i // 先默认currentIndex作为最小index
            for (var j = i; j < arr.length; j++) {
                // 每次筛选出最小val的下标
                if (arr[j] < arr[minIndex]) {
                    minIndex = j
                }
            }
        }
    
        if (minIndex !== i) {
            swap(arr, i, minIndex)
        }
        return arr
    }
    

# 3. 插入排序

时间复杂度：O(n2)。

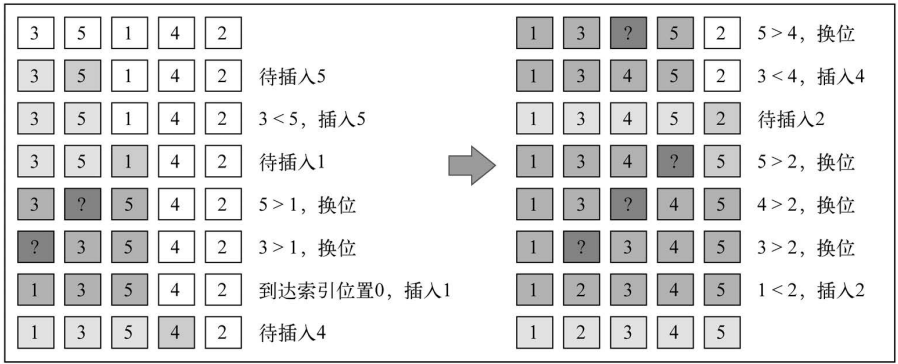
将一个元素插入到其它已经有序的牌中的适当位置，因此其他所有元素在插入之前都向右移动一位，为新元素腾出空间。有点类似摸扑克牌排序。

如果对一个已经有序的数组使用插入排序，插入排序只会遍历数组一遍，时间复杂度退化为 O(n)；可以想象，如果对一个接近有序的数组使用插入排序，其效率是非常可观的，而很多时候我们处理的数据是接近有序的，只需调整一些无序项，所以插入排序是很有用的。

    function insertSort(arr) {
        for (var i = 1; i < arr.length; i++) {
            var j = i
            var temp = arr[j] // 待排序值，0-（j-1）已经排好序列
            while(j > 0 && arr[j - 1] > temp) {
                arr[j] = arr[j - 1] // j - 1的值，往后挪，给temp值留位置
                j-- // 循环继续判断
            }
            arr[j] = temp // 找到考察的数应处于的位置
        }
        return arr
    }
    

排序小型数组时，此算法比选择排序和冒泡排序性能要好。

# 4. 归并排序

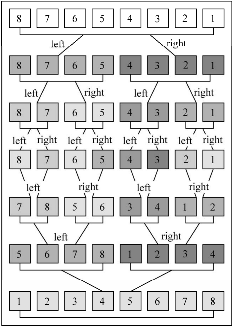
前三种算法性能都不好，归并排序是第一个可以被实际使用的排序算法。时间复杂度：O(nlogn)。

使用left和right两个数组存储，每次循环都减少一半（但也每次多两个变量数组），空间换时间。

从数组的中间拿一个值，然后通过这个值挨个和数组里面的值进行比较，如果大于的放一边，小于的放一边，然后把这些合并，再进行比较，如此反复即可。

    function mergeSort(arr) {
        if (arr.length <= 1) return arr
    
        // 取中间index/value
        var index = Math.floor(arr.length / 2)
        var middle = arr.splice(index, 1)
    
        var left = [], right = []
        for (var i = 0; i < arr.length; i++) {
            var cur = arr[i]
            cur > middle ? right.push(cur) : left.push(cur)
        }
    
        // 递归调用left/right快排
        return mergeSort(left).concat(middle, mergeSort(right))
    }
    

# 5. 快速排序

最常用的排序算法，时间复杂度：O(nlogn)，性能通常比其他复杂度为O(nlogn)的排序算法高。

和归并排序一样，使用分治的方法，将原始数组分为较小的数组（但没有像归并那样将他们分割开,没有占据额外的空间）。

1. 从数组选择一项作为主元（一般有头/中间/尾三种算法选择）
2. 划分操作：创建两个指针，分别指向头和尾，移动左指针和右指针，双方一个大于一个小于时，交换。这样在一次循环中，在主元中左边都比主元小，右边都比主元大。
3. 重复2

# 1. 选择头作为主元：

    function quickSort(arr) {
        quick(arr, 0, arr.length - 1)
    }
    
    function quick(arr, left, right) {
        if (arr.length <= 1) return
        if (left >= right) return
    
        // 基于主元，把合理的val左右互调，以及确定好主元的位置。
        var index = partition_By_First(arr, left, right)
    
        // 剩下的继续递归
        quick(arr, left, index - 1)
        quick(arr, index + 1, right)
    }
    
    let partition_By_First = function(arr, i, j) {
        let pivot = arr[i] // 取第一个作为主元
        while(i < j) {
            if (arr[i + 1] < pivot) {
                a[i] = a[i+1] // 小于，则往左边堆，i+1 后退
                i++
            } else {
                swap(arr, i + 1, j) // 大于，则跟右边互换
                j--
            }
        }
        a[i] = pivot // i即为最终的基元位置（分割点）
        return i
    
        // // 以上代码等价于wiki快排的以下代码：
        // let pivot = arr[i]
        // while(i < j) {
        //     while(arr[i] < pivot) {
        //         i++
        //     }
        //     while(arr[j] > pivot) {
        //         j--
        //     }
    
        //     if (i <= j) {
        //         swap(arr, i, j)
        //         i++
        //         j--
        //     }
        // }
        // a[i] = pivot // i即为最终的基元位置（分割点）
        // return i
    }
    

# 2. 选择中间作为主元：

    function quickSort(arr) {
        quick(arr, 0, arr.length - 1)
    }
    
    function quick(arr, left, right) {
        if (arr.length <= 1) return
        if (left >= right) return
    
        var index = partition_By_Middle(arr, left, right)
    
        // 剩下的继续递归
        quick(arr, left, index - 1)
        quick(arr, index, right)
    }
    
    function partition_By_Middle(arr, i, j) {
        var pivot = arr[Math.floor((i + j) / 2)]
        while(i < j) {
            while(arr[i] < pivot) {
                i++
            }
            while(arr[j] > pivot) {
                j--
            }
    
            if (i <= j) {
                swap(arr, i, j)
                i++
                j--
            }
        }
        return i // left作为和right的交汇点，返回
    }